PINBALL TROUBLE-SHOOTING
PART 6
BASIC CIRCUITS
CONTINUED
By Russ Jensen
Russ Jensen concludes his explanation of the electrical circuits and how they work that was begun in the July issue of The Coin Slot. These principles, when understood, will be of great value to a collector trying to diagnose mal functions in a pinball game.
MORE CIRCUIT THEORY
In the first part of this series the basic electrical circuit was defined. It was said to be a "series" circuit, in that electric current would flow from a power source, through a switch (either simple or complex, as we discussed last month) if it were closed, and finally through a load that would perform some function. All these components have been described in great detail in the past several months. It is now time to tie them all together in an actual circuit and discuss the basic electrical laws that govern the operation of any such circuit
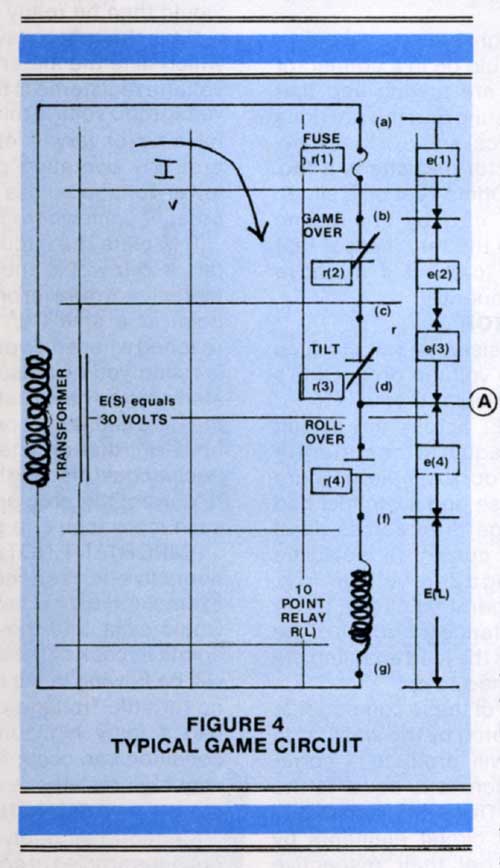
Figure 4 represents a simple game circuit, in which a rollover switch (normally open) is used to energize a relay (10 Point Relay) in order to score 10 points. A portion of the common switches (the normally closed "Game Over" and "Tilt" relay switches), which control the application of power to some of the game's circuits are also shown as well as the fuse in the coil power line. All of these circuit elements are shown, because in order for electric current to get to the load (relay coil) it must pass through each of them.
Disregarding for the moment the notations in Figure 4 enclosed in boxes, you will notice that the coil power secondary of the game's transformer is shown. It is indicated that this produces a voltage of 30 volts, which I have labeled "E(S)" (more on notation shortly). A circular arrow is also shown, labeled I, indicating the flow of electric current through the entire "series" circuit (from transformer through the fuse, switches and load, and back, to the transformer). Finally, you will notice the notation "R(L)" next to the relay coil, which indicates the resistance of the coil to the flow current. It should be noted that no current will flow until the normally open rollover switch is closed,
There is a fundamental law of electrical circuit theory, known as Ohm's Law, that can be represented by the formula I equals E/R. This says that the amount of current (I") flowing in any circuit is equal to the voltage ("E") of the source divided by the resistance ("R") to current flow in the circuit This law will be the basis for all the discussion to follow.
(NOTE: The notations "I," "E," and "R" (used for current, voltage and resistance respectively) may seem Strange but are traditional in Physics and Engineering. I have added (in parenthesis) additional modifiers to provide information about the quantities during this discussion For example: "E(S)" indicates source voltage and "R(L)" indicates resistance of the load.)
The Ohm's Law formula is presented here to illustrate the fact that two conditions can cause a decrease in the amount of current flowing in a circuit; a decrease in voltage supplying current to the circuit, or an increase in the resistance of that circuit to current flow. Of these two factors the latter is the most common in malfunctioning games. However, as will be pointed out later, an increase in resistance in one circuit can cause a decrease in voltage in another circuit fed by it
In a properly operating circuit, the current flowing will be determined only by the source voltage and the load's resistance (or impedance in the case of A.C. Circuits, see note below). In the example in Figure 4 this would be the case if there was no resistance presented by any of the circuit elements (fuse, switches, etc.) in the current path between the transformer and the load.
(NOTE: I have been using the term resistance generically to mean the resistance to the flow of current. Actually the resistance as defined in Physics and Engineering, refers to the property of circuit elements that resists equally both D.C. (direct current) and A.C. (alternating current). Certain circuit elements (in the case of games, coils and motors) have an additional resistance to the flow of A.C. only. which is due to their electromagnetic properties and is known as reactance. The sum of these two resistances (resistance and reactance) is called impedance. This impedance would be used in the Ohm's Law formula for coils and motors in A.C. circuits only, in place of "R(L)," and would be labelled "Z(L)" to differentiate it from other true resistances in the circuit
If any of the circuit elements (other than the load, of course) have resistance, this will add to the resistance of the circuit and thus decrease the current flowing, since in the Ohm's Law formula you are dividing the source voltage by a bigger "R" resulting in a smaller "I." If all these circuit elements (fuse, switches, etc.) are operating correctly they will have Zero (or close to it) resistance If, however, any of them are causing problems they can have some resistance, which I have denoted in Figure 4 by the small letters "r" (for example "r(l)").
The most common cause of unwanted resistance in game circuits is dirty or misadjusted switch contacts described in a previous article. A faulty switch can exhibit almost any resistance up to, of course, an open Circuit (infinite resistance). The possible resistances of the three switches shown in Figure 4 are indicated as "r(2)," r(3) and "r(4)." A perfect switch, when closed, would have zero resistance, although a properly operating switch can have a very small resistance because nothing is perfect!
Figure 4 also indicates (by "r(1)") that the fuse can have resistance. Actually, the fuse itself has a very small resistance that can be ignored, but what I intended to point out is that the fuse holder can exhibit a resistance if the fuse does not fit firmly into the metallic holding clips that provide its electrical contacts. This is often a problem in malfunctioning games and should be checked. The fuse clips should be cleaned and bent together so they make good, firm contact with the ends of the fuse.
While we're on the subject of poor contact causing unwanted resistance, a common and irksome cause of this phenomena should be mentioned, that of poor contact in 'quick disconnect" connectors. The typical circuit in a game usually involves components physically located in various areas of the machine (such as playfield, backbox and bottom of the cabinet). In order that the backbox and playfield can be removed, the manufacturers have provided' quick disconnect' connectors in the wiring for all circuits that go from one area to another (playfield to backbox, playfield to cabinet, etc.).
The wiring connecting a typical circuit, such as the one in Figure 4, may involve several of these connectors in order to connect all of the components together in a circuit. Although this wiring is somewhat difficult to trace (wire color codes must be used, and connectors are not indicated on most schematics) it must be done in many instances during troubleshooting a game. If a bad connection is found, the mating contacts must be cleaned and the socket adjusted for a tight fit with the mating plug pins.
THE ZERO OHMS TEST
Now that we know that various conditions in a game can cause unwanted resistance in a circuit, how do we detect it, and if it exists, isolate its cause(s)? One way (another method will be discussed later) is by what I call the Zero Ohms Test To perform this test you must have a Volt/Ohm Meter, which can be purchased at any electronics store for as little as $20. This is an essential tool in game servicing. When used as an Ohmmeter (one of its selectable functions) it measures resistance (the kind that affects both AC. and D.C. circuits, but not reactance, see note above) in units of Ohms.
(NOTE: Zero Ohms is a short circuit, meaning there is no resistance to the flow of current. Higher values indicate increased resistance to current flow, an open circuit having an infinite resistance, or no current flow.)
To use the Ohmmeter for measuring resistance you must first select the Ohms function and the lowest resistance scale (usually called "R x 1") meaning that the resistance in Ohms can be read directly from the meter's "Resistance Scale'). The needle on the meter should immediately go to the high end of the scale (infinite resistance) since you have an open circuit between the meter leads. Next, short the two leads together, and the meter should return to near Zero, since you now have a short circuit between the meter leads. Most meters provide an adjusting know, (usually labeled 'Ohms Adjust’), which can be used to place the meter exactly on Zero. If Zero cannot be reached, the meter's internal batteries should be replaced. You are now ready to perform the test on one of the game's circuits. (WARNING! the game should be unplugged when any Ohm-meter testing is being performed or damage to the meter may result)
Figure 4 will be used as an example of a typical circuit on which the Zero Ohms Test is to be performed. You would first attach one of your meter leads (using a clip lead) to the terminal on the fuse socket whose wire provides current from the transformer (wire color codes and the schematic must be used to determine this). This point in Figure4 is labeled "(a)." Next, you would attach the other lead of the meter to the relay coil terminal (point labeled "f” in Figure 4) This is the terminal on the coil that is not connected to the coil common power line. Your meter should read infinite resistance (top of scale) since the rollover switch is open. (NOTE: In this example the fuse is shown »n the side of the coil power line that feeds the switches. In many games the coil common line is fused instead. In these cases a separate Zero Ohms Test should be performed between that side of the transformer and the coil common side of the coil to test for unwanted resistance in the fuse socket and any intervening connectors.)
The rollover switch would next be closed manually, at which time the meter should go to Zero Ohms. As stated earlier, in a properly operating game a small resistance is normal, but anything over 1/4 Ohm should be suspect. If the meter indicates unwanted resistance, the meter lead attached to the coil (point “f” ) should be moved to point "d." If Zero Ohms is then obtained your problem would be in the circuitry just eliminated (in this case either the rollover switch or any intervening 'quick disconnect' connectors).
If, however, you still did not get 'Zero, keep moving your meter lead back one point in the circuit (to point "c," then "b," etc.) until you locate the faulty part of the circuit. You should then correct the problem (clean and adjust the faulty switch or connector), and then retest everything as two faults could have existed, one masking the other.
A word of warning! Your test might seem to indicate a faulty switch yet the problem could be in a connector that is between the point you are testing and that switch. So if the point you are testing and the previous point tested are in different physical areas of the game, look for the intervening connector and check it too (HINT: You can perform a Zero Ohms Test on a single component (switch, connector, etc.) by connecting your two meter leads directly to the terminals of that component This is a good way to check if you have properly fixed a fault in a component.)
VOLTAGE DROP
The presence of unwanted resistance will produce an effect on a circuit known as voltage drop. Ohm's Law can also be stated by the formula "E equals l x R.” This means that the voltage (E) across any circuit element will have a resistance (R) that is equal to the current (I) multiplied by the resistance. If, in our example in Figure 4, all of the circuit elements (fuse and switches) had Zero resistance then the voltage drop across all of them would be Zero since the current (I) would be multiplied by Zero, thus producing a Zero voltage drop. This means that in a properly operating circuit, all (or almost all, remember some resistance is normal) of the supply voltage will appear across the load enabling the load to operate as it was designed to do.
If. on the other hand, any or all of these components have unwanted resistance (denoted by the small "r" in the boxes in Figure 4) they will produce a corresponding voltage drop, "e(4)," across it, equal to the current, "I," multiplied by "r(4)." The same idea would hold true for any of the other circuit elements by multiplying their "r" by "I" to get their respective voltage drops ("e").
The result of all of this would be that the voltage appearing across the load ("E(L) in Figure4) would be the source voltage, "E(S)," MINUS the sum of all the individual voltage drops of the circuit components ("e(1)" plus "e(2)" plus "e(3)" plus "e(4)"). Thus the larger the voltage drops (produced by larger, unwanted resistances) the less voltage will be supplied to the load, causing it to operate marginally or not at all. This voltage drop is thus a symptom of the situation where unwanted resistance is present in a circuit
The phenomena of voltage drop provides the basis for another test to determine the presence of unwanted resistance in a circuit, the Voltage Drop Test. This test is similar to the Zero Ohms Test, except it is performed with the game's power on and voltages, rather than resistances, are measured with the Volt/Ohm meter.
The circuit of Figure 4 will again be used as an example. To perform a Voltage Drop Test on that circuit you would first start the game (so that the "Game Over" relay would be in its normal, unoperated, condition). Your Volt/Ohmmeter would be set up for the 'A.C. Volts' function and the lowest voltage scale selected that has as its maximum voltage reading a voltage over 30 Volts( '50 Volt Scale,' for example). One of the meter leads would be connected to the side of the coil connected to the coil common power line (point 'g" in Figure 4). The other meter lead should be connected to the other side of that coil (point "f"). You would then be ready to perform the test.
Next the rollover switch must be closed by hand, at which time the meter should register a voltage. If the voltage registered is the same as the transformers coil voltage(30 volts in this example), or very close to if you have no (or very little) voltage drop and your circuit is probably operating properly. If, however, you get a lower voltage across the coil unwanted resistance is present somewhere in the circuit.
To isolate the circuit component causing the resistance you would then proceed by moving your one meter lead (the one on point "f) back in the circuit one point at a time ("d," then "c," etc.), until a point is reached where full voltage is obtained. When this point is found you have isolated the problem to the circuit element you have just eliminated, just as in the case of the Zero Ohms Test previously described. Don't forget, however, that an intervening 'quick disconnect connector could also bet he culprit The next step would be to correct the problem and retest the entire circuit in case more than one problem existed.
(IMPORTANT NOTE: While performing this test all normally open switches (only the rollover switch in this example) must be held closed. If not, an open circuit would exist and the full voltage would appear at all points in back of the open circuit because no current component had a fairly high unwanted resistance. This same condition can occur if a normally closed switch has a very high resistance or is completely open.)
COMMON POWER CIRCUITS
Mention has been made several times in this and previous articles of common power circuits, which feed more than one circuit in a game. An example of such a circuit could be that part of the circuit of Figure 4 between the upper side of the transformer winding and point "d" (including the fuse and the normally closed contacts of the "Tilt" and "Game Over" relays). You will notice that I have indicated a line, labeled "A," which represents the common point where other circuits fed by this common circuit would be connected. We shall now consider, using Ohm's Law, the effects on the game of malfunctions in this type of common circuit
If (in addition to the rollover switch and 10 Point Relay circuit shown) other circuits were attached to point "A" (in order to obtain power) each of these circuits would use a certain amount of current to operate. The behavior of electrical circuits is such that the total current flowing through the common circuit would be the sum of all the individual currents flowing in the circuits fed by it. You can also see, from the previous discussion of voltage drop, that the larger the current in this common circuit the larger the voltage drop between the transformer and point "A” resulting from any unwanted resistance in this common circuit. The resulting voltage at point "A" would be the transformer voltage, "E(S)," MINUS the voltage drop through the common circuit components.
The resulting voltage at point A" can be considered as the supply voltage to each of the individual circuits fed by the common circuit As you can see, the lower this supply voltage to a circuit the less chance that circuit has to operate properly. Now, since the individual circuits attached to point "A" are, for the most part, being turned on and off (sometimes drawing current and sometimes not) during operation of the game, the resulting current flow through the common circuit is hence the supply voltage to the individual circuits) is also changing. It should be plain to see that this condition can result in intermittent problems occurring in the game's operation.
It should be kept in mind that all these problems can only occur if there is unwanted resistance (caused by a malfunction) in one or more of the components in the common circuit If all components in this circuit had Zero (or very little) resistance, the voltage drop across them would be Zero (or very small) no matter how much current (le. one or many circuits operating) was flowing. A good test to see if this type of problem is occurring is to use a voltmeter to monitor the voltage at the common connection point (point "A" in the example) during actual playing of the game, to see if the voltage fluctuates to any great degree (say more than ten percent). If it does, then either the Zero Ohms Test or the Voltage Drop Test can be used to isolate the cause of the problem (the components) having unwanted resistance).
This concludes the discussion of circuit theory. While at first it may seem highly technical, the principles are really quite simple and logical and. when understood, are of great value in enabling one to understand why things happen as an aid to diagnosing malfunctions in a game. Next month some typical types of circuits will be described, and their operation will be discussed step-by-stepi
Correction
In the July issue of The Coin Slot an error was made in Russ Jensen's article, "Pinball Troubleshooting, Part 6, Basic Circuits." Some copy was inadvertently left out of the third paragraph, first column on page 39, the note about parallel switches. This paragraph should have read:
(NOTE: If more than two switches are connected in "parallel," their function would be the functions of each switch connected by OR. For example: two normally open switches ("A" and B") and one normally closed switch ("C") connected in "parallel" would have the function "A" OR " B" OR NOT "C." This would appear to be reasonable, since for current to flow in a "parallel circuit any one switch need only be closed.)
We apologize to Russ and our readers for this error and hope it has caused no inconvenience.